Today, I will present the CPU to you. This article commences with an analogy to elucidate the basics of CPU design. I trust this has provided a clearer understanding of the CPU for you.
Have you ever pondered that each time you return home and illuminate the room, you are essentially creating a sophisticated CPU with a mere push of a switch? However, the quantity required for such a CPU would be significantly higher, reaching into the billions.
I. An extraordinary innovation
What stands out as the most pivotal invention of the past two centuries for humanity? Is it the steam engine? Perhaps the advent of electric light? What about the rocket? It’s highly likely that none of these claims the top spot, and arguably, one of the most essential inventions is:
A transistor is the term for this diminutive device. You might be curious about the purpose of a transistor.
In reality, the function of a transistor is so elementary that it can’t get any simpler. If one end is powered on, the current can flow through the other two ends; otherwise, the current is blocked, making the device essentially a switch.
The discovery of this tiny component led three individuals to be awarded the Nobel Prize in Physics, underscoring its significance.
Regardless of how intricate the program crafted by the programmer is, the simple act of opening and closing this small object is what ultimately carries out the functions executed by the software. I find myself at a loss for words and can only think of it as “magic.”

A transistor is the term for this small device. You might be curious about the purpose of a transistor.
In reality, the function of a transistor is so basic that it can’t get any simpler. If one end is powered on, the current can flow through the other two ends; otherwise, the current is blocked, making the device essentially a switch.
The discovery of this tiny component led three individuals to be awarded the Nobel Prize in Physics, underscoring its significance.
Regardless of how intricate the program crafted by the programmer is, the simple act of opening and closing this small object is what ultimately carries out the functions executed by the software. I find myself at a loss for words and can only think of it as “magic.”
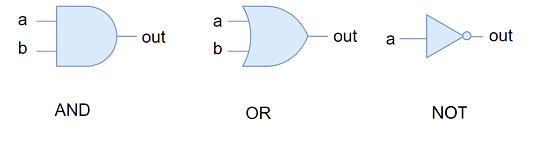
Ⅱ. AND, OR, NOT
Now that you have a transistor, which is a switch, you can easily create these three combinations because you can build blocks on this basis:
The current will only pass, and the light will turn on if both switches are turned on at the same time.
The current can flow, and the light will be on as long as one of the two switches is turned on.
When the switch is closed, the current flows through the light and it is on; when the switch is opened, the current cannot flow, and the light is turned off.
Ⅲ. Two in one, three in two, three in all
An astonishing aspect is that you can represent any logic function by employing AND, OR, and NOT gates in any of the three circuit types you randomly design. This phenomenon is referred to as logical completeness, and it is truly remarkable.
In essence, any logic function can be achieved using a sufficient number of AND, OR, and NOT gates, without the need for other types of logic gate circuits. Currently, we consider AND, OR, and NOT gates to be logically complete.
The conclusion drawn in this paper signals the onset of the computer revolution. This deduction suggests that computers can be constructed using basic AND, OR, and NOT gates, and these uncomplicated logic gate circuits share similarities with genes.
Tao begets one, one begets two, two begets three, and three begets all things, as per Lao Tzu.
Is it truly necessary to execute every logical operation exclusively with AND, OR, NOT gates, even though it is achievable with them? Clearly not, and it is also impractical.
Ⅳ. How does computational power originate?
We embarked on the task of constructing the fundamental capability of the CPU: computation, utilizing addition as an illustration. With the emergence of the NAND gate, the elemental component capable of generating anything, we began developing the most crucial capacity of the CPU: computation.
Considering that the CPU recognizes only 0 and 1 in binary, what are the binary addition combinations?
0 + 0 results in 0, with a carry of 0;
0 + 1 results in 1, with a carry of 0;
1 + 0 results in 1, with a carry of 0;
1 + 1 results in 0, with a carry of 1—binary!
Observe the carry column closely. The carry is 1 only when the values of the two inputs are 1. Examine the three circuits you crafted using combinational logic. The AND gate is precisely what its name suggests. Is there any doubt?
Revisit the result column once more. When the two inputs have disparate values, the result is 1, and when they share the same value, the result is 0. Does this sound familiar? It’s XOR! As established, the NAND or NOR gate is logically complete and can produce any outcome. XOR logic, naturally, poses no challenge. Binary addition can be accomplished with an AND gate and an XOR gate:
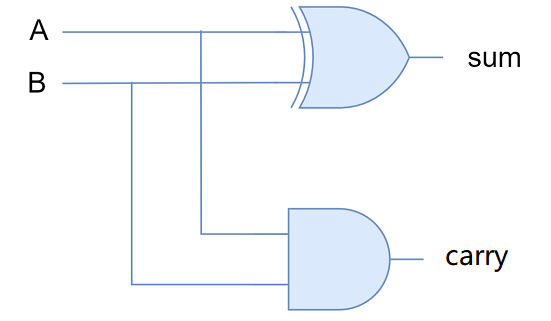
The provided circuit serves as a basic adder, and whether it is perceived as magical is subjective. NOR gates are versatile, not only enabling addition but also facilitating other functions. The logical framework is now complete.
Beyond addition, we have the flexibility to create various arithmetic operations as needed. The circuit dedicated to performing these calculations is referred to as an arithmetic/logic unit, or ALU, and the CPU module responsible for these operations essentially mirrors the simple circuit mentioned earlier. There’s no distinction; it’s just more intricate.
Presently, computer power is harnessed by amalgamating NOR gates, illustrating how computational capability is achieved.
However, computational power alone is insufficient; the circuit must also possess the capacity to retain information.
Ⅴ. Remarkable Memory Capability
Up until this point, the combinational circuits you’ve constructed, like adders, lacked a means to retain data. They simply generate output based on input, but both the input and output require a location to store information, necessitating the incorporation of a circuit for this purpose.
How can information be effectively stored in circuits? Designing this seems elusive, causing restless contemplation. Thoughts about it permeate your daily activities—while eating, walking, and even squatting—until one day, you chance upon a British scientist in your dream. In a moment of revelation, he imparts some advice and presents a circuit akin to yours: simple yet truly enchanting:
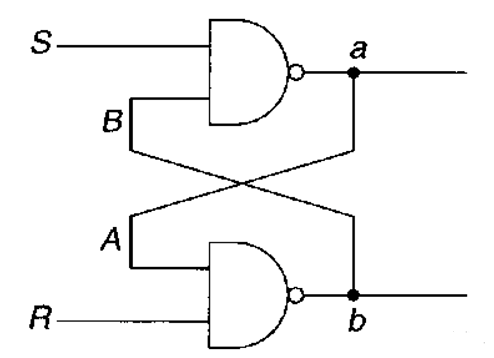
Don’t fret; this is a combination of two NAND gates, just like how NAND itself is a combination of NAND gates that you previously constructed. The NAND gate involves first performing an AND operation and then negating the result. When given inputs 1 and 0, the output of the AND operation is 0, and the output of the NOT operation is 1. This defines the NAND gate, with the other components being inconsequential.
The uniqueness of the circuit lies in its combination. The output of one NAND gate serves as the input for two other NAND gates. This combination bestows an intriguing characteristic upon the circuit. As long as 1 is supplied to the S and R segments, there are only two possible outcomes:
If the a side is 1, then B=0, A=1, b=0;
If the a side is 0, then B=1, A=0, b=1;
With no other alternative, we consider the value of terminal a as the circuit’s output.
Subsequently, if you set the S terminal to 0 (while the R terminal remains 1), the circuit’s output—i.e., the a terminal—is consistently 1. At this juncture, we can assert that 1 has been stored in the circuit. Conversely, if the R segment is set to 1 (while S remains 1), the circuit is reset, and its output—i.e., the a terminal—is invariably 0. We can affirm that 0 is stored in the circuit at this point.
Irrespective of whether you perceive it as magical or not, the circuit possesses the capacity to store data.
Now, to retain the information, both the S and R terminals must be set, yet you already have one input (which stores a bit). Therefore, you’ve made a simple modification to the circuit:

Ⅵ. The Emergence of Registers and Memory
Now that your circuit can store a single bit, expanding the storage to accommodate multiple bits isn’t a straightforward task; a simple solution is to duplicate and replicate:
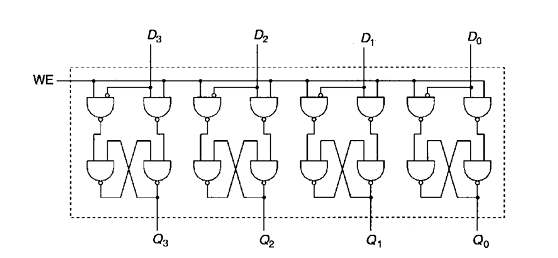
We designate this combinational circuit as a register. Yes, you read that correctly. This is the register, as we refer to it.
If this doesn’t suffice, you must proceed to construct more intricate circuits to store additional data and incorporate addressing functions, thereby giving rise to the concept of memory.
Registers and memory are intricately connected to the uncomplicated circuit discussed in the previous section. Information is retained in this circuit as long as the power is on, but it is evidently lost when the power is turned off. This clarifies why memory cannot preserve data once the power is disconnected.
Ⅶ. Hardware or software?
Our circuits are now capable of computing data and storing information, yet a challenge persists: even though we can express all logic functions using AND, OR, and NOT, we still need to encompass all logic operations in our circuits. Can it be accomplished with an AND-NOR gate? This is simply implausible.
For computational logic, corresponding hardware need not be implemented for all operations. Only the most fundamental functions are demanded from the hardware. Ultimately, these foundational functions can be utilized to articulate any computer logic in software. This is known as the software paradigm. As per conventional wisdom, hardware is immutable, but software is adaptable. The hardware remains constant, yet different software can empower the system to execute new functions.
Humans are indeed remarkably astute. Next, let’s delve into how hardware furnishes these so-called basic functions.
Ⅷ. Basics of hardware
Consider this: how does the CPU know that it is tasked with adding two integers and which specific numbers to add?
Clearly, you must communicate this information to the CPU. How do you achieve that? Remember the chef’s recipe from the preceding section? That’s right; the CPU requires a set of instructions to determine its next action. In this case, the recipe takes the form of machine instructions, executed by the combinational circuit created earlier.
Now, another quandary arises: there should be a plethora of these instructions, which is impractical. Take the addition instruction, for instance; you could have the CPU calculate 1+1, 1+2, and so forth, but in reality, there’s only the addition instruction. There are countless conceivable combinations, and the CPU would undoubtedly be unable to execute them all.
In essence, the CPU only needs to offer the addition operation; you supply the operand. The CPU asserts, “I can hit people,” and you instruct it whom to hit; the CPU declares, “I can sing,” and you tell it what to sing; the CPU says, “I can hit people,” and you provide the target. The CPU announces, “I can cook,” and you furnish the details.
Consequently, it becomes apparent that the CPU merely provides methods or functions (such as hitting, singing, cooking, adding, subtracting, and jumping), while you provide strategies (whom to hit, song name, dish name, operand, jump address).
The instruction set serves as the framework for implementing the CPU’s expression mechanism.
Ⅸ. Instruction Set
The instruction set delineates the operations the CPU can perform, along with the operands required for each instruction. The instruction sets of different CPUs exhibit variation.
Typically, the presentation is akin to this: The instructions in the set are inherently straightforward, often appearing like this:
Read a number from memory, with “abc” representing the address;
Add two integers together;
Check if a number is greater than six;
Store this number at the address “abc” in memory.
Etc.
It may seem like a jumble of thoughts, but these are instructions for the machine. A program composed in a high-level language, such as sorting an array, eventually transforms into equivalent instructions like those mentioned above. These instructions are then executed sequentially by the CPU.
The initial four bits of this instruction inform the CPU that it constitutes an addition command, indicating that the CPU’s instruction set can accommodate 24 or 16 machine instructions. The remaining bits specify the CPU’s action, instructing it to add the values in register R6 and register R2 and store the result in register R6.
As evident, machine instructions can be cumbersome, prompting contemporary programmers to craft programs in high-level languages.
Ⅹ. Conductor: Let’s Play a Song
Despite our circuit now possessing computation, storage, and the capability to dictate operations through instructions, a challenge remains unresolved.
Our circuit comprises various components for calculation and storage. Take the simplest addition, for instance. Suppose we want to compute 1+1, with these two numbers residing in the R1 and R2 registers, respectively. It’s crucial to note that registers can store data. How do we ensure that when the adder begins its operation, both R1 and R2 hold 1 and not any other values?
In essence, what serves as the basis for synchronizing or coordinating the diverse components of the circuit to work harmoniously? Similar to how a conductor is indispensable for a symphony performance, our computational combinational circuits require one too.
This conducting role is fulfilled by the clock signal.
In the conductor’s hand, the clock signal acts like a baton. When the baton is wielded, the entire orchestra responds with a unified action. Likewise, each register in the entire circuit (representing the entire circuit’s state) undergoes an update whenever the voltage of the clock signal changes, ensuring that the entire circuit functions in harmony.
Now, you should comprehend the significance of the CPU’s main frequency. The primary frequency is essentially the number of times the baton is waved in a second. The higher the primary frequency, the greater the number of operations the CPU can execute within a single second.
At this point, we have an ALU capable of performing diverse calculations, a register capable of storing data, and a clock signal governing their interactions. The amalgamation of all these components is collectively referred to as the Central Processing Unit, or CPU for short.